Stability SOS

CMU 16-715: Advanced Robot Dynamics & Simulation - Fall 22.
🆘 Stability Verification Using Sum-of-Squares Programming

This is my project within the course 16-715: Advanced Robot Dynamics & Simulation at Carnegie Mellon University in Fall 2022 semester. Some key points:

Stability Verification via SOS | Python, Drake, Mosek | [pdf] [slides]

  • Verified the Lyapunov stability of dynamical systems by formulating and solving sum-of-squares programs with Mosek, compared with Drake.
  • Implemented and compared three different approaches; sample-based method gained tighter solution 30 times faster than standard one.

Abstract—We explore sampling-based sum-of-squares (SOS) programming as a technique to verify the stability of nonlinear systems. We provide a review of Lyapunov analysis, traditional SOS stability verification, and sampling-based SOS verification, then apply these methods to two nonlinear systems. We demonstrate that sampling-based SOS verification offers significant advantages over the traditional formulation in terms of problem size and the amount of time required to obtain a solution. The code for this project is available at link.

For more details, please check our report.

Introduction

Deploying robots into dangerous environments and environments with humans requires ensuring that their operation is safe. One control-theoretic notion of safety is stability–the property that within some range of operating conditions, the robot can be trusted to track desired trajectories or drive itself to a desired operating point. Recently, there has been a great deal of work in verifying stability using sum-or-squares (SOS) programming, which expresses Lyapunov stability conditions as nonnegativity conditions for sets of polynomials. A problem with the traditional SOS approach is its scalabiltiy to higher-dimensional systems, particularly due to its reliance on high-degree Lagrange multiplier polynomials for representing constraints, leading to large semidefinite programs. This is restrictive since there are many intriguing real-world applications that are far larger than 10-15 states, such as mechanical systems made up of several rigid bodies. Various techniques have been used to address this problem, e.g. DSOS and SDSOS programming.

In this project, we examine a recent sampling-based method of SOS programming that addresses the scalability problem in [html], and compare it to the traditional SOS approach.

Methods

Lyapunov Stability Analysis

Suppose we have the following autonomous dynamical system

\[\dot{x} = f(x)\]

and want to verify the asymptotic stability of the origin \(x = 0\). These dynamics might represent the closed-loop dynamics of a controller attempting to drive the system’s state to the origin. Lyapunov analysis proceeds by searching for a Lyapunov function V that satisfies the following two conditions:

\[V(x) > 0, \dot{V}(x) < 0\]

If such a function exists, then the origin x = 0 is asymptotically stable. For many systems, however, the origin is only stable within some region of attraction (ROA).

Stability Verification via Sum-of-Squares Programming

SOS stability analysis makes the assumption that \(V\) and \(f\) are polynomial functions of x. In practice, we formulate candidate Lyapunov functions \(V\) using the system’s total energy or the value function of an LQR controller, which are already polynomial. If the dynamics \(f\) are not polynomial, we can approximate them as polynomial using a Taylor expansion.

Binary search with SOS program.

Stability Verification via Sampling-based Sum-of-Squares Programming

Beside the popular SOS programming formulation described above, which is based on inequality implication (4), Sprocedure and multipliers, there is also an equality-constrained formulation. Define an algebraic variety as the set of solutions to a set of polynomial equations. The number of equations in the variety is the number of components. The core idea behind sampling-based SOS verification is that instead of solving the optimization problem for all real-valued \(x\), we only solve it at a set of numerical samples \(\{x_i\}\) in the algebraic variety.

Sampling-based SOS program.

Results

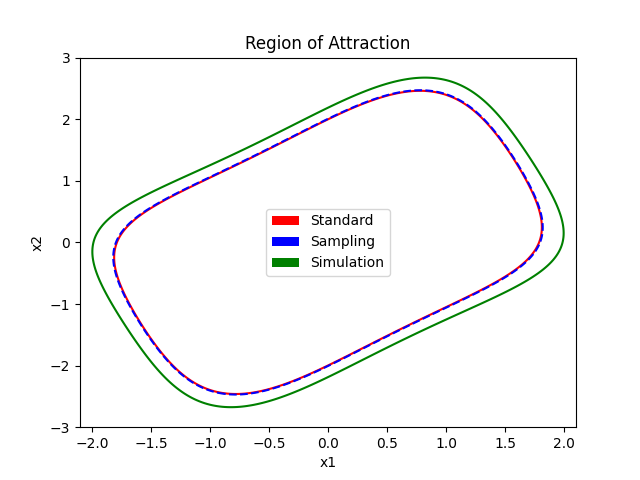
We verify both standard and sample-based methods derived above by comparing solve time and ROA values compared to ground truth which could be found by rolling out closed-loop system simulations. Van der Pol is a 2 state, degree 3 polynomial system.

We first simulate the system on an interesting grid for a certain amount of time. In this way, stable states could be found within some tolerances. The result from simulationbased verification is described in the Figure. Intuitively, if one needs better quality ROA using simulation, the complexity would increase exponentially with respect to problem dimension, grid size and converging time. This is why SDP programs are preferred for this ROA application. While the standard SOS program is not trivial to set up, the samplingbased one is simpler but in need of an efficient sampling method. The samples must be well-distributed, generic and not close to zeros (trivial solution) to find a non-zero ROA. Both programs are solved with Mosek using a degree 4 candidate V , resulting in good approximations. If the degree of the candidate V is increased, tighter ROA approximations could be found.

Van der Pol ROA approximations. Both programs produce qualitatively similar results

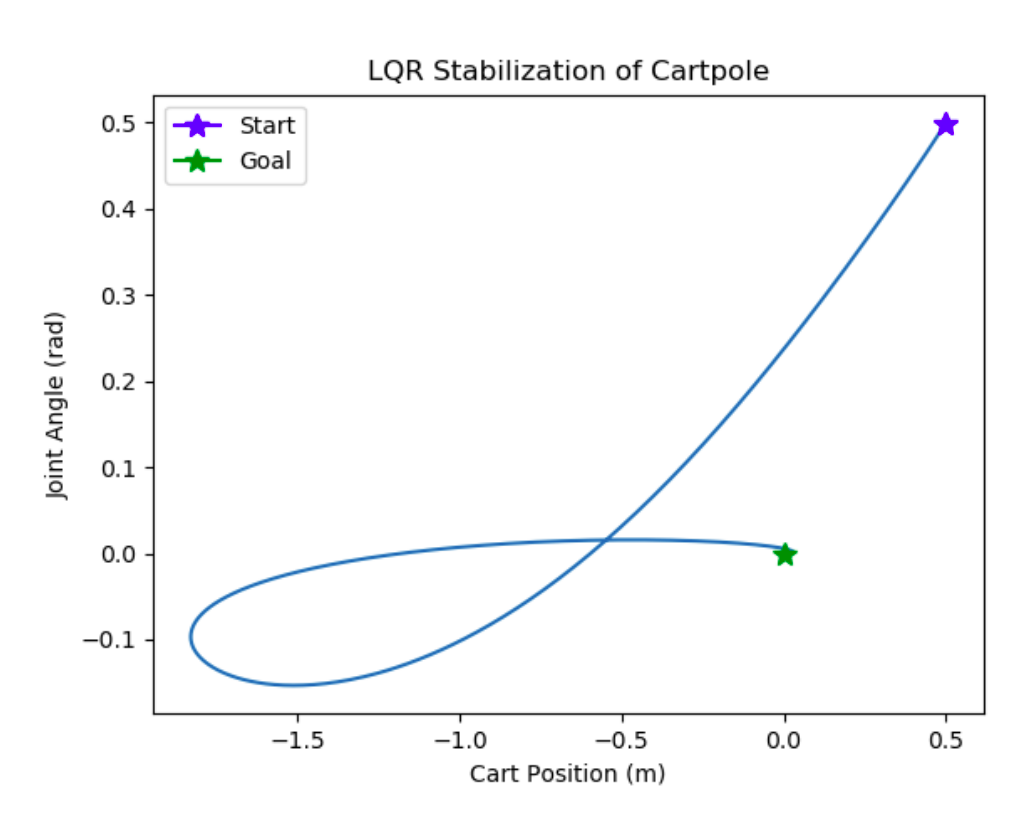
We also applied sampling-based SOS verification to an N-link cartpole. We assume that the cart, as well as all joints, except for the \(N\)th joint, are actuated, linearize the dynamics in the original coordinates, and design an infinite-horizon LQR controller \(\tau(q, v)\) to drive the full cartpole state, consisting of configuration and velocity, to zero. The trajectory induced by the controller from a perturbed initial condition, in the plane of the cart position and joint angle (\(N = 1\) here).

Cartpole regulation to origin, shown in plane of cart position and joint angle

Conclusions

In this project, we compared a recent sampling-based variant of SOS stability verification to a more traditional form of SOS stability verification, applied to a Van der Pol oscillator. Ground truth for the system was found by using simulationbased method. We found that the sampling-based variant produced a smaller program and took less time to solve. It may also provide less conservative ROA compared with the standard approach. We also applied sampling-based SOS verification to an N-link cartpole. Future directions of research include applying the sampling-based verification to higherdimensional systems. In particular, systems with contacts would be an interesting application, since they require many multipliers with the traditional SOS formulation, creating large SOS programs.