TinyMPC

This is my project within the course 16-715: Optimal Control & Reinforcement Learning at Carnegie Mellon University in Spring 2023 semester. Some key points:

TinyMPC: A Model Predictive Control for Embedded Applications | C/C++, Julia, Python, Crazyflie, STM32, Teensy | [pdf] [slides]

• Led a team to develop a novel efficient convex model-predictive control algorithm targeting embedded systems.
• Introduced a new full-state quaternion-based LQR/LQI controller onto Crazyflie (C/C++ on STM32); accomplished robust hovering performance.
• Evaluated the augmented Lagrangian-based MPC solver on Teensy Arduino and STM32F4.

Abstract—We introduce a novel model predictive control (MPC) framework designed for running on low-resource hardware. Our approach utilizes an Augmented Lagrangian-iLQR optimization method to handle trajectory optimization and constraint management. The framework is optimized to run on several microcontrollers, including the Teensy 4.1, STM32F401, and the Crazyflie 2.1 drone, which uses an STM32F405 processor. We detail the algorithm implementation, hardware optimization techniques, and provide a comparison of the framework’s runtime performance with other state-of-the-art solvers. Additionally, we present the results of testing the framework on the Crazyflie 2.1 drone, which shows that it can solve the full-state quadrotor problem with a minimum frequency of 16Hz, while a complementary LQR is implemented to stabilize the drone at 50Hz.

For more details, please check our report.

Introduction

In recent years, significant strides have been made in the field of robotics, particularly in deep learning (DL) and reinforcement learning (RL), resulting in a range of improved capabilities and applications. However, these advanced techniques often demand significant computing resources, which can pose challenges for many robotic applications. This stands in contrast to a significant portion of robotics that utilizes embedded systems with severely limited computing resources. These systems include palmsized toy robots like the Crazyflie quadrotor and the Petoi Bittle quadruped, as well as mission-critical robots like NASA’s Mars Perseverance rove. The Crazyflie and Bittle employ affordable and accessible commercial microcontrollers, such as families of STM32 and Teensy, respectively. Meanwhile, the Perseverance rover relies on RAD750, a radiation-hardened version of the PowerPC 750 processor from the previous century. Clearly, the need for resource-constrained robotic applications is widespread. Operating within a tight computational budget, these embedded systems require innovative approaches to enable the efficacy of advanced techniques.

Our contributions to the field of optimal control are three-fold. Firstly, we have developed a highly efficient and extensible open-source optimal control solver in C. Secondly, we have created a user-friendly MPC interface that simplifies the setup and compilation of our solver on various hardware platforms. Finally, we have provided benchmark results to demonstrate the efficacy of our approach and a hardware demonstration to showcase its practicality.

Design

Constrained Optimal Control Problem

Up to this point, we have not considered any constraints on the state x or input u. Real-world systems have many types of physical or desired limitations. Some popular constraints are box constraints on the state and input at each time step (to ensure that the solution is realizable on hardware and to encourage smoothness in the solution), equality constraints on the goal state (to ensure that that a desired final position is reached), and second-order cone constraints to, for example, enforce thrust limits.

To handle constraints, we use the augmented Lagrangian method (ALM) which enforces constraints into the cost function. Generally, our tracking problem is convex, and a global solution can be found with only one constrained backward pass. However, multiple iterations are needed to satisfy dual feasibility. Below is the pseudo-code of our AL-TVLQR algorithm.

Note the subtle difference between AL here and in iterative LQR (iLQR). In iLQR, one will naturally approximate the cost with second-order Taylor expansion about the current trajectory, then group the cost in gradient and Hessian terms, not precisely like linear and quadratic terms like ours. Third-rank tensors are ignored. Moreover, one will solve the backward pass and forward pass iteratively until convergence so that any mismatch due to nonlinearity can be eliminated. Constraints have to be in linear form so they can be substituted and grouped into corresponding terms.

The TinyMPC Framework

Functions to compute state and control matrices were generated using Symbolics.jl in Julia by symbolically compute the Jacobians of the given robot’s dynamics function with respect to the state control variables. These symbolic functions were converted to C functions. Reference trajectories were generated using ALTRO and similarly copied into C code format for use on a microcontroller.

We use the SLAP (Simple Linear Algebra Protocols) library developed by Dr. Brian Jackson for matrix computations. SLAP was chosen because it is tested and lightweight and because of our architectural decision to have as few dependencies as possible. We modified SLAP, to replace the backend of some of the most commonly used functions with existing implementations that are much faster and can be precompiled for use with SLAP.

Results

After having verified the correctness of our algorithm by comparing it with the solution from ALTRO in Julia, we chose to implement our algorithm on three common and accessible microcontrollers as a demonstration of the range of embedded systems on which our solution can run. We chose to implement our algorithm on a Teensy 4.1, an STM NucleoF401RE, and an STMF405 on a Crazyflie 2.1. The Crazyflie drone is a common research platform for autonomous and distributed swarm algorithm research. We chose to use it because it is small and thus has fast attitude dynamics that we want to show can be stabilized by TinyMPC.

Speed Increases

After profiling our C implementation, we found the algorithm was spending around 77% of its time in the SLAP, the library we used as our matrix processing backend. Specifically, the algorithm was in the matrix add and multiply function around 75% of the time. This function multiplies two matrices, multiplies them by a scalar, then sums the result with a third matrix multiplied by a second scalar to produce a final result. To speed up our implementation, we replaced the original SLAP implementation with Eigen 3.1 matrices. This adds a new dependency to our implementation, but since it is added as a backend to the SLAP library, users can simply download a precompiled version of SLAP and not need to worry about downloading and compiling Eigen themselves. Replacing the SLAP backend with Eigen halved the runtime of our MPC function, allowing us to run the dynamic bicycle model in real time (faster than 50Hz) with a horizon length of 4 knot points. This speed increase is still not enough to run the quadrotor at 50Hz, even with only two knot points in the horizon.

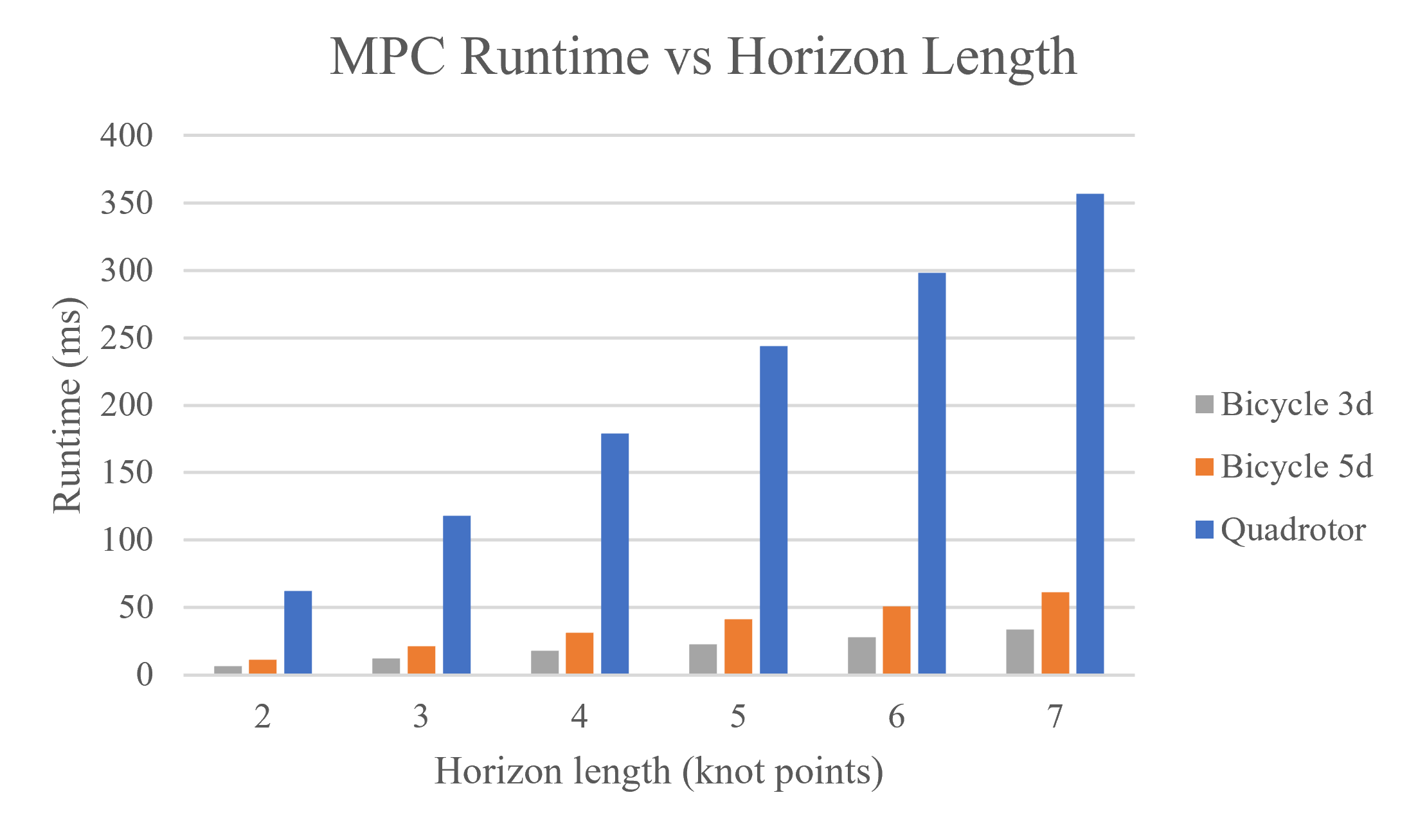
Variable Sampling Time

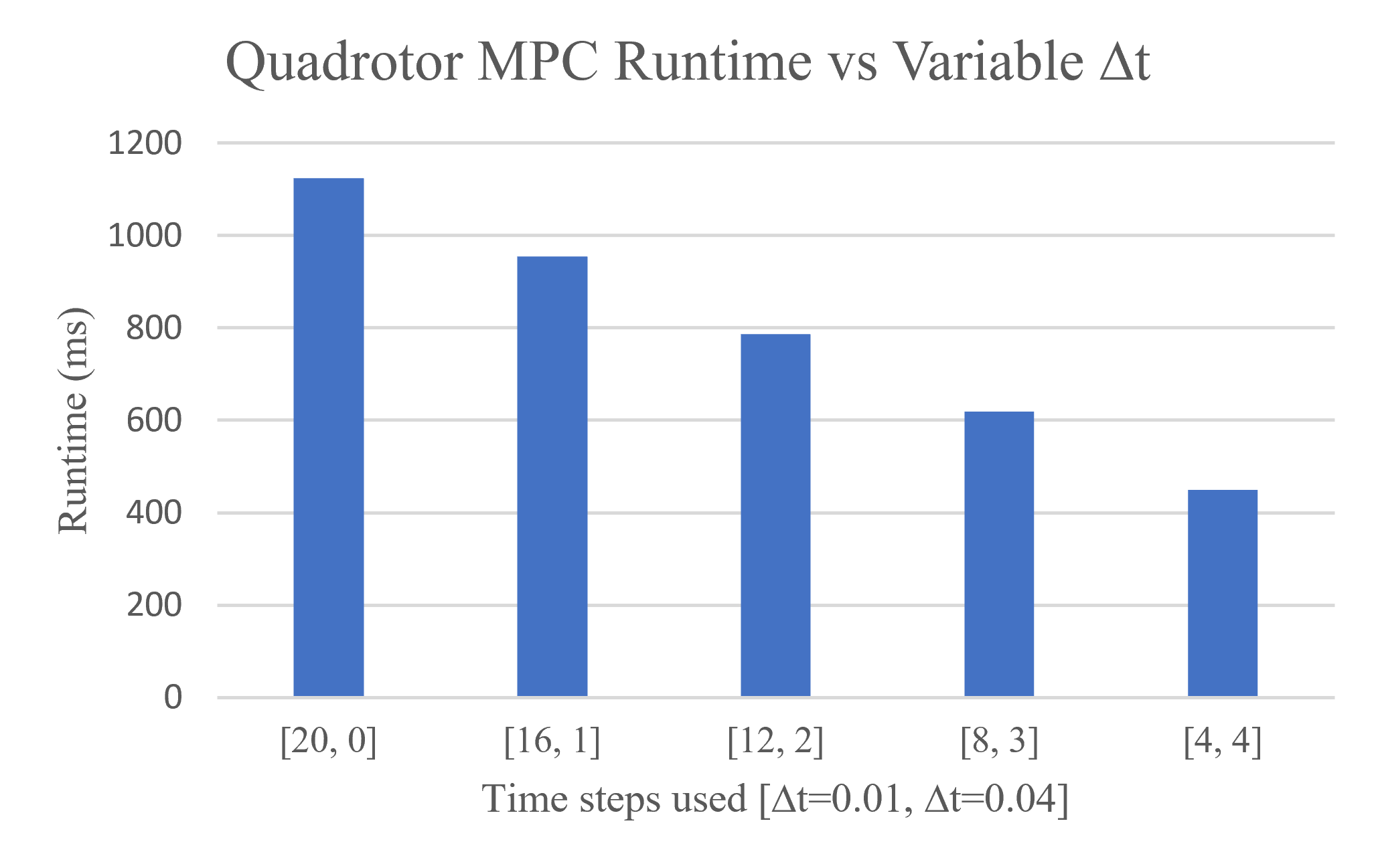
We take advantage of the constantly updating nature of MPC and the fact that knot points farther into the future do not have to be predicted as accurately as those closer to the current state of the robot by increasing the time step for later knot points. This allows the MPC algorithm to cover the same amount of horizon time using fewer knot points, decreasing runtime while achieving similar performance. This works primarily because the fast dynamics of the system need to be stabilized immediately while obstacle avoidance, which relies more on computing the position of the robot, generally has slower dynamics and thus can be computed using a larger time step. On the quadrotor, this was implemented by linearizing two dynamics functions about hover, one with the initial fast time step and one with the slow time step used for the remainder of the horizon time.

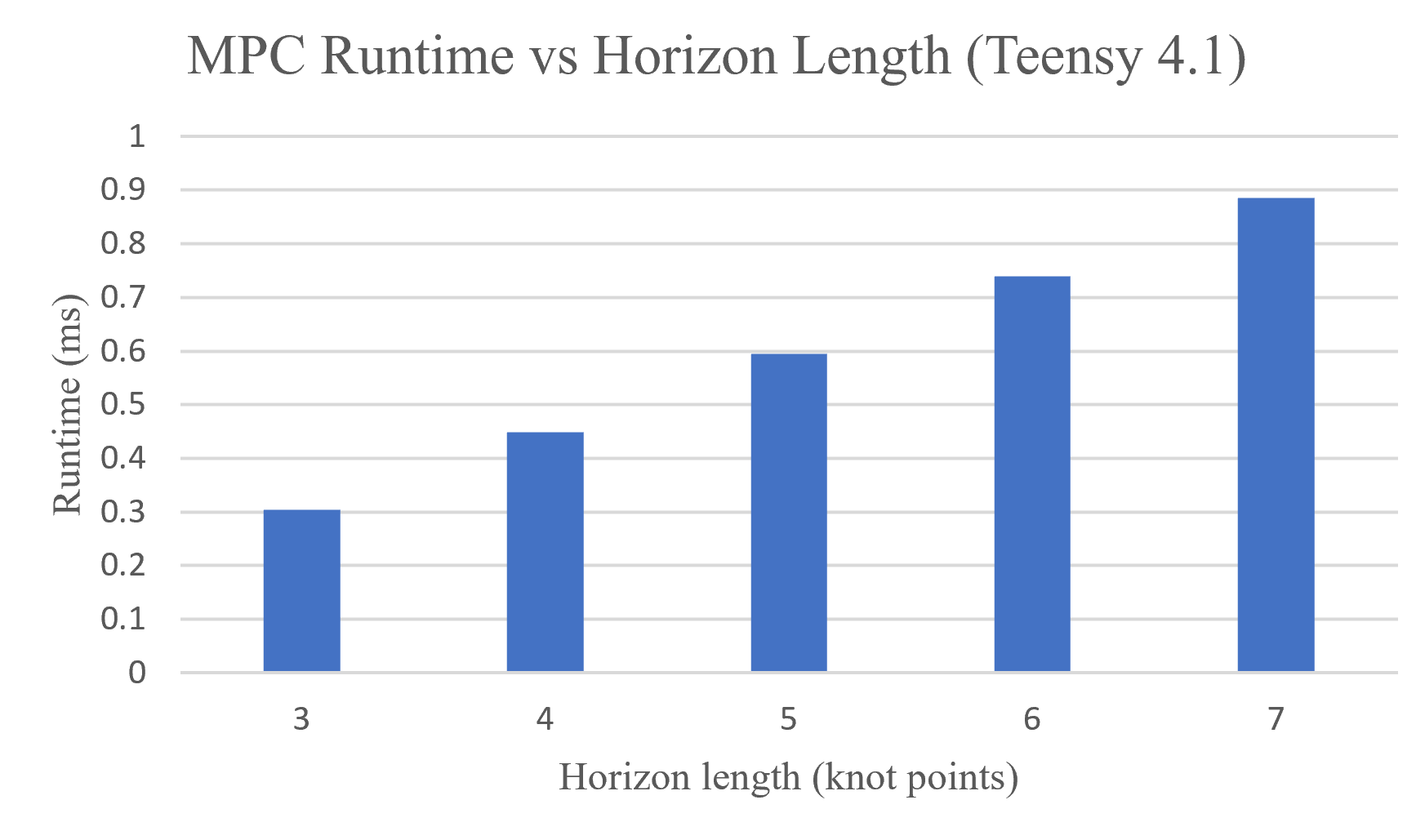
The results in figures show results from running on the STM NucleoF401RE. The F401RE uses a Cortex M4 processor running at a maximum clock frequency of 16 MHz. The function runtimes from this processor are far too slow to be run on the Crazyflie quadrotor. The exact same code was run on a Teensy 4.1 in a fraction of the time. The Teensy 4.1 uses a Cortex M7 chip that, in our tests, was run at a clock frequency of 600 MHz. This is the highest natively supported clock frequency that does not require active cooling. The Teensy ran our MPC code in under 1 millisecond for each horizon length shown in the figure. With 130 knot points for the horizon length, the Teensy ran the function in 20 milliseconds, which is an MPC runtime frequency of 50Hz. This is the same frequency used to control the drone using LQR, and is promising given we’re able to run the Cortex M4 on the Crazyflie at the speed of the Teensy 4.1.

Because our MPC algorithm does not yet run fast enough to control a quadrotor, we opted to solve for the infinite horizon LQR gains for the model we obtained from Bitcraze, the developers of the Crazyflie, and implement our own controller on their software stack. Directly copying the optimal gain matrix obtained from infinite horizon LQR caused the drone to exhibit a stable, sinusoidal wobbling behavior during flight. This wobbling was removed by handtuning the optimal gain matrix. We then generated position and velocity knot points for a figure-8 trajectory we wanted the drone to follow. Although the drone did not follow the trajectory properly, it did stay in the air for the duration of the trajectory.

Conclusions

The hardware results above highlight the computational complexities of running an MPC algorithm in real-time on an underpowered micro controller. We have demonstrated that our algorithm may run in real-time on devices like the Teensy 4.1 which runs on a Cortex M7 processor running at up to 1GHz. There is still work to do to demonstrate these results on power and resource constrained devices such as the Crazyflie 2.1 running a Cortex M4 chip. We have not yet reduced the runtime of our algorithm to the point where it may be run on the Crazyflie’s processor in real-time, but there are a few things we can implement to speed up our algorithm. Our future work is proposed as below:

Algorithm: We plan to create a new version of the solver using ADMM rather than AL to help reduce the required online computation. ADMM will require fewer matrix-matrix multiplications (from matrix factorizations), which is primarily what is slowing down our code.

Conic Constraints: We have attempted to incorporate conic constraint handling, but this is still a work in progress.

Model Hierarchy Predictive Control: An additional method implemented to increase performance is a hierarchical dynamics model scheme, where the first few time steps use the full model dynamics and the remainder use increasingly simplified versions of the robot’s dynamics. This can be done for similar reasons as variable sampling time. Doing this reduces the computational complexity of the Jacobians for later time steps which decreases overall runtime. Time steps closer to the first horizon knot point require higher-accuracy dynamics to correctly determine the robot’s future state, but later time steps only need to look at low frequency dynamics since the higher frequency dynamics will likely be incorrectly estimated anyway. These low frequency dynamics tend to be attributed to much simpler models, such as point mass models, and can be used to determine a subset of the robot’s state farther into the future, such as its center of mass. Often, center of mass is all that is required when trying to avoid obstacles farther into the future.

Code Generation: Following applications like OSQP, Simulink, and SLinGen, we would like to be able to generate C code from a higher level programming language. The overhead of extra work required to do this pays off in the form of a much simpler user interface and being able to optimize for a wide variety of specific platforms using a single program.

Based on this class project, we keep developing TinyMPC and achieve great success. Check out tinympc.org.